
Problems with Detailed SolutionsĪn object is launched at a velocity of 20 m/s in a direction making an angle of 25° upward with the horizontal.Ī) What is the maximum height reached by the object?ī) What is the total flight time (between launch and touching the ground) of the object?Ĭ) What is the horizontal range (maximum x above ground) of the object?ĭ) What is the magnitude of the velocity of the object just before it hits the ground?Ī projectile is launched from point O at an angle of 22° with an initial velocity of 15 m/s up an incline plane that makes an angle of 10° with the horizontal. An interactive html 5 applet may be used to better understand the projectile equations. These problems may be better understood when Projectile problems are presented along with detailed solutions. Thus from the above observation, we conclude that, the angle of projection would be 60 o. Substituting the values from equations (1) and (2), we get, Let θ be the angle of projection and u its initial speed. The speed of a projectile when it is at its greatest height is √2/5 times its speed at half the maximum height. The images are then moved down and to the right to show the independence of horizontal and vertical motion. A camera takes a picture of the flight every second on the same frame of film. Refer this simulation for projectile motion:-Ī ball is launched at an angle and lands at the same height it is launched from. This is the equation of trajectory which is a parabola (y = ax + bx 2).

Then x = u cos θ.t and y = u sin θ.t - 1/2 gt 2Įliminating 't' form the above equations, we get, Let P (x, y) be the position of the particle at instant after t second. Refer this video for better understanding about projectile motion:-Īssuming the point of projection as the origin of co-ordinates and horizontal direction as the x-axis and vertical direction as the y-axis. Horizontal Range (OA=X) = Horizontal velocity × Time of flightĪt the highest point of the trajectory, vertical component of velocity is zero. Use equation b.Īs t cannot equal to zero, then, total time of flight, When body returns to the same horizontal level, the resultant displacement in vertical y-direction is zero. Here we use different equation of motions of one dimension derived earlier to get the different parameters. Velocity and accelerations can be resolved into two components: (b) Along the horizontal x-axis with a uniform velocity forward.Ĭonsider a particle projected with an initial velocity u at an angle θ with the horizontal x-axis as shown in figure shown below. (a) Along the vertical y-axis with a uniform downward acceleration 'g' and
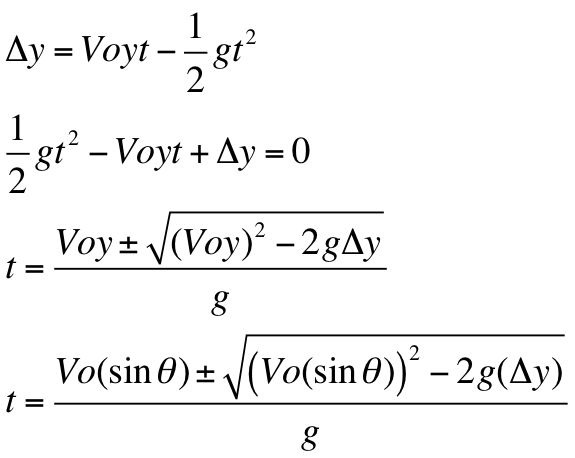
Hence it is easier to analyze the motion of projectile as composed of two simultaneous rectilinear motions which are independent of each other: To analyze the projectile motion we use the following concept "Resolution of two dimensional motion into two one dimension motion" as discussed earlier. Now we discuss some example of curved motion or two dimensional motion of constant acceleration such as the motion of constant acceleration such as the motion of a particle projected at certain angle with the horizontal in vertical x-y plane (this type of motion is called projectile motion). Air resistance to the motion of the body is to be assumed absent in this type of motion.Ī body projected into the space and is no longer being propelled by fuel is called a projectile. Concepts of Physics by HC Verma for JEE.IIT JEE Coaching For Foundation Classes.


 0 kommentar(er)
0 kommentar(er)
